23년 1월 29일 모각코
계획 -> 딥러닝 Practical Gradient Descent Methods
학습결과 ->
Gradient의 세가지 분류
- Stochastic gradient descent
하나의 샘플을 통해서만 gradient를 계산해서 업데이트 하는 것
- Mini-batch gradient descent
batch size(128개, 256개 등)의 샘플을 한번에 사용해서 gradient를 구해 업데이트 하는 것
대부분의 딥러닝에서 활용
- Batch gradient descent
한번에 모든 샘플을 사용해서 gradient 평균을 사용해 업데이트 하는 것
Batch-size Matters
Large Batch-size를 활용하면 Sharp Minimum에 도달, Small Batch-size 사용하면 Flat Minimum
Sharp Minimum보다는 Flat Minimum에 도달하는 것이 더 좋음
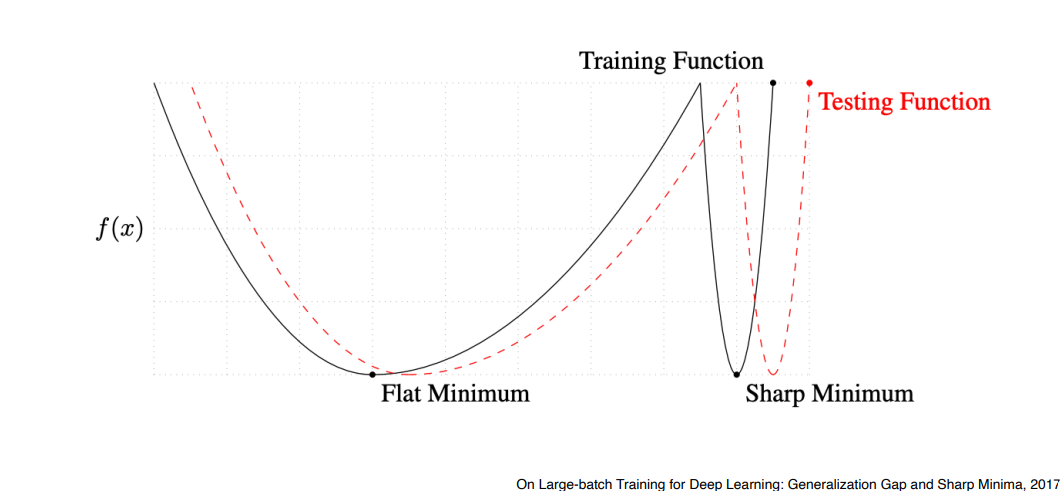
목적은 Test Funtion의 minimum을 찾는것
Flat minimum의 특징은 Training Function에서 조금 멀어져도 Testing Function에서 적당히 낮은 값이 나옴 -> Training 데이터에 잘 되면 Test 데이터에서도 어느정도 잘 됨 (Generalization Performance가 높음)
Sharp Minimum 같은 경우 조금만 멀어져있어도 Test Function에서 높은 값이 나옴 (Generalization Performance 가 떨어짐)
Gradient Descent
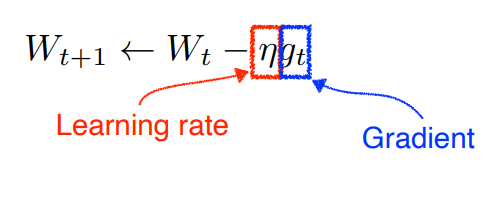
w는 neural network의 weight
문제점 : learning rate를 잡는게 어려움. 너무 크면 학습이 안되고 너무 작으면 아무리 학습시켜도 학습이 안됨.
Momentum
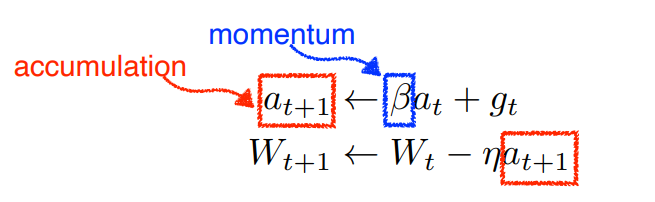
한번 gradient가 어떤 방향으로 흐르면 다음번 gradient가 조금 다른 방향으로 흘러도 그 전의 방향으로 흐르던 정보를 조금 이어나가겠다.
beta라고 불리는 하이퍼파라미터가 momentum(관성)을 잡게되고 g라고 불리는 gradient가 현재 들어왔다면 다음번(t+1)번째에 momentum이 포함된 gradient로 업데이트
장점 : 한번 흘러가기 시작한 방향을 어느정도 유지시켜주기 때문에 gradient가 왔다갔다해도 어느정도 잘 학습이 되는 효과
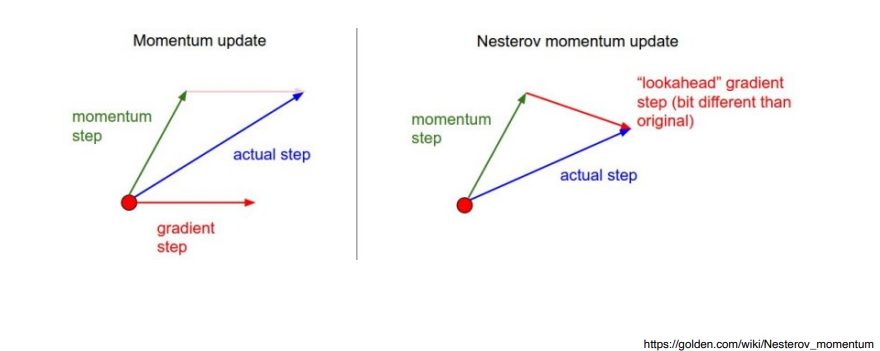
Nesterov Accelerated Gradient (NAG)
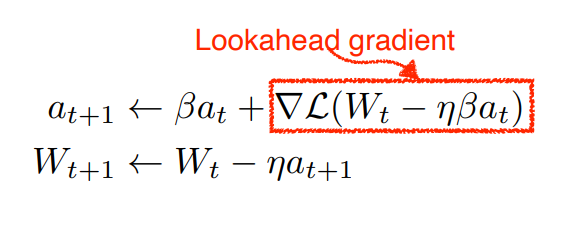
a라고 불리는 현재 정보가 있으면 그 방향으로 한번 가보고 그 간 곳에서 gradient를 계산한걸 가지고 accumulation을 함
Adagrad
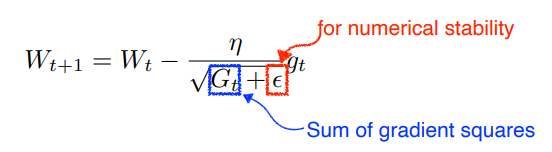
neural network의 파라미터가 지금까지 얼마나 변해왔는지를 봄
많이 변한 파라미터에 대해서는 더 적게 변화시키고, 적게 변한 파라미터에 대해서는 더 많이 변화시키겠다
G는 지금까지 gradient가 얼마나 많이 변해왔는지를 제곱해서 더한 값 (계속 커짐)
G가 역수이기 때문에 G가 크면 더 적게, 작으면 더 많이 변화시킴
문제점 : G가 계속 커지기 때문에 무한대로 가면 W에 업데이크가 안됨 -> 뒤로 가면 갈수록 학습이 점점 멈춰짐
Adadelta

Adagrad의 문제점인 Gt가 계속 커지는 현상을 최대한 막는 방법
현재 타임스텝 t가 주어졌을 때 얘를 어느정도 윈도우 사이즈 만큼의 파라미터 시간에 대한 gradient 제곱의 변화를 보겠다
윈도우 사이즈를 백으로 잡으면 이전 백개동안에 g라는 정보를 들고 있어야해서 많은 양의 파라미터가 들어가 있는 모델을 쓰면 엄청난 양의 파라미터를 들고있어야 해서 터짐
이걸 막을수 있는 방법이 EMA(exponential moving average)
특징 : 러닝레이트가 없어서 바꿀수있는 요소가 많이 없어서 많이 활용안함
RMSprop
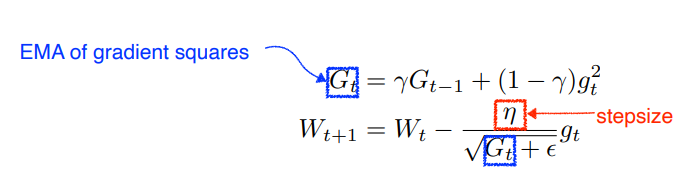
gradient squares을 그냥 더하는게 아니라 EMA를 더해줌
대신 eta라는 stepsize가 들어감
Adam(Adaptive Moment Estimation)
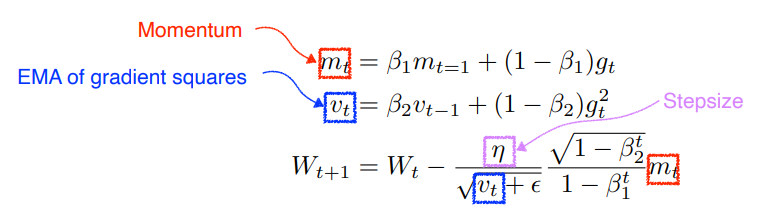
가장 잘되고 무난하게 사용됨
EMA of gradient squares와 Momentum을 같이 활용함
gradient의 크기가 변함에 따라서 혹은 gradient square의 크기에 따라 adaptive하게 learning해서 바꾸는 것과 이전의 gradient 정보에 해당하는 momentum 정보를 잘 합친 것
하이퍼파라미터로는 β1(momentum을 얼마나 유지시킬지에 대한 것), β2(gradient squares에 대한 EMA 정보), η(learning rate), ε가 있음. 이 네개의 파라미터를 조정하는 것도 매우 중요
실제로는 division by zero를 막기 위한 ε(입실론) 값을 잘 바꿔주는게 중요